HIPERBÓLICAS

Definiciones de Funciones Hiperbólicas

senh(x) = ( e ^x - e ^-x )/2

csch(x) = 1/senh(x) = 2/( e ^x - e ^-x )

cosh(x) = ( e ^x + e ^-x )/2

sech(x) = 1/cosh(x) = 2/( e ^x + e ^-x )

tanh(x) = senh(x)/cosh(x) = ( e ^x - e ^-x )/( e ^x + e ^-x )

coth(x) = 1/tanh(x) = ( e ^x + e ^-x)/( e ^x - e ^-x )

cosh ²(x) - senh ²(x) = 1

tanh ²(x) + sech ²(x) = 1

coth ²(x) - csch ²(x) = 1

Definiciones de Funciones Hiperbólicas Inversas

arcsenh(z) = ln( z + (z ² + 1) )

arccosh(z) = ln( z 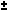(z ² - 1) )

arctanh(z) = 1/2 ln( (1+z)/(1-z) )

arccsch(z) = ln( (1+(1+z ²) )/z )

arcsech(z) = ln( (1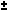(1-z ²) )/z )

arccoth(z) = 1/2 ln( (z+1)/(z-1) )

Relaciones con las Funciones Trigonometricas

senh(z) = -i sen(iz)

csch(z) = i csc(iz)

cosh(z) = cos(iz)

sech(z) = sec(iz)

tanh(z) = -i tan(iz)

coth(z) = i cot(iz)