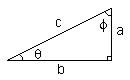
| sen(theta) = a / c | csc(theta) = 1 / sen(theta) = c / a |
| cos(theta) = b / c | sec(theta) = 1 / cos(theta) = c / b |
| tan(theta) = sen(theta) / cos(theta) = a / b | cot(theta) = 1/ tan(theta) = b / a |
sen(-x) = -sen(x)
csc(-x) = -csc(x)
cos(-x) = cos(x)
sec(-x) = sec(x)
tan(-x) = -tan(x)
cot(-x) = -cot(x)
| sen^2(x) + cos^2(x) = 1 | tan^2(x) + 1 = sec^2(x) | cot^2(x) + 1 = csc^2(x) | |
sen(x 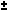 y) = sen x cos y y) = sen x cos y 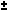 cos x sen y cos x sen y | |||
cos(x 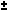 y) = cos x cosy y) = cos x cosy 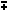 sen x sen y sen x sen y | |||
tan(x 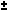 y) = (tan x
y) = (tan x 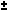 tan y) / (1
tan y) / (1 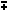 tan x tan y)
tan x tan y)
sen(2x) = 2 sen x cos x
cos(2x) = cos^2(x) - sen^2(x) = 2 cos^2(x) - 1 = 1 - 2 sen^2(x)
tan(2x) = 2 tan(x) / (1 - tan^2(x))
sen^2(x) = 1/2 - 1/2 cos(2x)
cos^2(x) = 1/2 + 1/2 cos(2x)
sen x - sen y = 2 sen( (x - y)/2 ) cos( (x + y)/2 )
cos x - cos y = -2 sen( (x-y)/2 ) sen( (x + y)/2 )
| ángulo | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| sen^2(a) | 0/4 | 1/4 | 2/4 | 3/4 | 4/4 |
| cos^2(a) | 4/4 | 3/4 | 2/4 | 1/4 | 0/4 |
| tan^2(a) | 0/4 | 1/3 | 2/2 | 3/1 | 4/0 |
Dado un triángulo abc, con ángulos A,B,C; a está opuesto a A; b opuesto a B; c opuesto a C,
a/sen(A) = b/sen(B) = c/sen(C) (La Ley del Seno)
| (La Ley del Coseno) |
(a - b)/(a + b) = tan 1/2(A-B) / tan 1/2(A+B) (La Ley de la Tangente)

















No hay comentarios:
Publicar un comentario