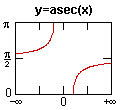sábado, 19 de diciembre de 2009
TRASFORMADAS
f(x) = e^(-xt) g(t) dt (Transformada de Laplace)
f(x) = e^(-xt) g(t) d(t) (Transformada de Laplace-Stieltjes)
f2(x) = L{L{g(t)}} = g(t)/(x+t) dt Transformada de Stieltjes
Transformada de Fourier
f(x) = 1/(2) g(t) e^(i tx) dt (Transformada de Fourier)
f(x) = (2/) g(x) cos(xt) dt (Transformada Coseno)
f(x) = (2/) g(x) sin(xt) dt (Transformada Seno)
Tranformada de Serie de Potencias
f(x) = (k=0..) g(k) x^k
LA SERIE FOURIER
a(0) / 2 + (k=1..) (a(k) cos kx + b(k) sin kx)
a(k) = 1/PI f(x) cos kx dx
b(k) = 1/PI f(x) sin kx dx
El residuo de la serie de fourier. Sn(x) = la suma de los primeros n+1 términos a x.
el residuo(n) = f(x) - Sn(x) = 1/PI f(x+t) Dn(t) dt
Sn(x) = 1/PI f(x+t) Dn(t) dt
Dn(x) = Dirichlet kernel = 1/2 + cos x + cos 2x + .. + cos nx = [ sin(n + 1/2)x ] / [ 2sin(x/2) ]
Teorema de Riemann. Si f(x) es continuo a excepción de un número finito de saltos finitos en todos los intervalos finitos pues:
lim(k->) f(t) cos kt dt = lim(k->)f(t) sin kt dt = 0
La serie fourier de la función f(x) en un intervalo arbitrario.
A(0) / 2 + (k=1..) [ A(k) cos (k(PI)x / m) + B(k) (sin k(PI)x / m) ]
a(k) = 1/m f(x) cos (k(PI)x / m) dx
b(k) = 1/m f(x) sin (k(PI)x / m) dx
El Teorema de Parseval. Si f(x) es continuo; f(-PI) = f(PI) pues
1/PI f^2(x) dx = a(0)^2 / 2 + (k=1..) (a(k)^2 + b(k)^2)
La Integral Fourier de la función f(x)
f(x) = ( a(y) cos yx + b(y) sin yx ) dy
a(y) = 1/PI f(t) cos ty dt
b(y) = 1/PI f(t) sin ty dt
f(x) = 1/PI dy f(t) cos (y(x-t)) dt
Casos Espaciales de la Integral Fourier
si f(x) = f(-x) pues
f(x) = 2/PI cos xy dy f(t) cos yt dt
if f(-x) = -f(x) then
f(x) = 2/PI sin xy dy sin yt dt
(Transforms) de Fourier
(Transform) Fourier Coseno
g(x) = (2/PI)f(t) cos xt dt
(Transform) Fourier Seno
g(x) = (2/PI)f(t) sin xt dt
Identidades de los (tranforms)
Si f(-x) = f(x) pues
Transform Fourier Coseno ( Tranform Fourier Coseno (f(x)) ) = f(x)
Si f(-x) = -f(x) pues
Transform Fourier Seno (Transform Fourier Seno (f(x)) ) = f(x)
TABLA DE FUNCIONES
gamma = la constante de Euler = 0.5772156649...
(x) = Gamma(x) = t (x-1) e -tdt (Función Gamma)
B(x,y) = t (x-1) (1-t) (y-1)dt (Función Beta)
Ei(x) = e -t/t dt (Integral Exponencial) ó una variente no eqivalente:
Ei(x) = + ln(x) + (e t - 1)/t dt = gamma + ln(x) + (n=1..inf)x n/(n*n!)
li(x) = 1/ln(t) dt (Integral del Logaritmo)
Si(x) = sen(t)/t dt (Integral del Seno) ó una variente no eqivalente:
Si(x) = sen(t)/t dt = PI/2 - sen(t)/t dt
Ci(x) = cos(t)/t dt (Integral del Coseno) ó una variente no eqivalente:
Ci(x) = - cos(t)/t dt = gamma + ln(x) + (cos(t) - 1) / t dt
Chi(x) = gamma + ln(x) + (cosh(t)-1)/t dt (Integral del Coseno Hiperbólico)
Shi(x) = senh(t)/t dt (Integral del Seno Hiperbólico)
Erf(x) = 2/PI (1/2)e (-t^2) dt = 2/PI (n=0..inf) (-1) n x (2n+1) / ( n! (2n+1) ) (Función de Error)
FresnelC(x) = cos(PI/2 t 2) dt
FresnelS(x) = sen(PI/2 t 2) dt
dilog(x) = ln(t)/(1-t) dt
Psi(x) = ln(Gamma(x))
Psi(n,x) = nth derivada de Psi(x)
W(x) = inverso de x*e x
L sub n (x) = (e x/n!)( x n e -x ) (n) (Polinomial de Laguerre, grado n; (n) significafo nth derivada)
Zeta(s) = (n=1..inf) 1/n s
Función Beta de Dirichlet B(x) = (n=0..inf) (-1) n / (2n+1) x
DENTIDADES DE INTEGRACIÓN
f(x) dx = lim (d -> 0) (k=1..n) f(X(k)) (x(k) - x(k-1)) cuando...
a = x0 < x1 < x2 < ... < xn = b
d = max (x1-x0, x2-x1, ... , xn - x(n-1))
x(k-1) <= X(k) <= x(k) k = 1, 2, ... , n
F '(x) dx = F(b) - F(a) (Teorema Fundamental para Integrales de Derivadas)
a f(x) dx = a f(x) dx (si a es una constante)
f(x) + g(x) dx = f(x) dx + g(x) dx
f(x) dx = f(x) dx | (a b)
f(x) dx + f(x) dx = f(x) dx
f(u) du/dx dx = f(u) du (integración por substitución)
TABLA DE INTEGRALES
xn dx = x(n+1) / (n+1) + C (n -1)
Demostración 1/x dx dx = ln|x| + C
Exponente / Logaritmo
ex dx = ex + C
Demostración bx dx = bx / ln(b) + C
Demostración
ln(x) dx = x ln(x) - x + C
Demostración
Trigonométrica
sen x dx = -cos x + C
Demostración cos x dx = sen x + C
Demostración tan x dx = -ln|cos x| + C
Demostración
csc x dx = - ln|csc x + cot x| + C sec x dx = ln|sec x + tan x| + C cot x dx = ln|sen x| + C
Resuelta Trigonométrica
cos x dx = sen x + C
Demostración sen x dx = -cos x + C
Demostración sec2 x dx = tan x + C
Demostración
csc x cot x dx = -csc x + C
Demostración sec x tan x dx = sec x + C
Demostración csc2 x dx = -cot x + C
Demostración
Trigonométrica Inversa
arcsen x dx =
1
(1-x2)
+ C
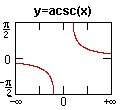
arccsc x dx =
-1
|x|(x2-1)
+ C
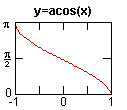
arccos x dx =
-1
(1-x2)
+ C
arcsec x dx =
1
|x|(x2-1)
+ C
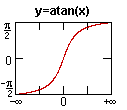
arctan x dx =
1
1+x2
+ C
arccot x dx =
-1
1+x2
+ C
Hyperbólica
senh x dx = cosh x + C cosh x dx = senh x + C tanh x dx = ln( cosh x ) + C
csch x dx = ln( tanh(x/2) ) + C sech x dx = atan( senh x ) + C coth(x) dx = ln( senh x ) + C
DISTRIBUCIONES
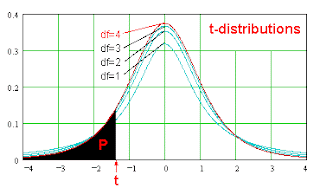
La distribución t, con n grados de libertad, está dada por la ecuación:
f(t) = [ ((n + 1)/2) (1 + x 2 / n) (-n/2 - 1/2) ] / [ (n/2) (PI n) ]
El z- es un N(0, 1) distributión, dando por la ecuación:
f(z) = 1/(2PI) e(-z^2/2)
El área encima de la intervalo (a,b) = normalcdf(a,b) = e-z^2/2 dz (No es integrable en forma algebraico.)
La expansión Taylor de lo aribo asiste en (speeding up) la el cálculo:
normalcdf(-, z) = 1/2 + 1/(2PI) (k=0..) [ ( (-1)^k x^(2k+1) ) / ( (2k+1) 2^k k! ) ]
Probabilidades Normal Estándar:
(La tabla baja es basando en el área P debajo de la Curva Probabilidad Normal Estándar, a la izquiera de la z-estadística respecta.)
z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09
-4.0 0.00003 0.00003 0.00003 0.00003 0.00003 0.00003 0.00002 0.00002 0.00002 0.00002
-3.9 0.00005 0.00005 0.00004 0.00004 0.00004 0.00004 0.00004 0.00004 0.00003 0.00003
-3.8 0.00007 0.00007 0.00007 0.00006 0.00006 0.00006 0.00006 0.00005 0.00005 0.00005
-3.7 0.00011 0.00010 0.00010 0.00010 0.00009 0.00009 0.00008 0.00008 0.00008 0.00008
-3.6 0.00016 0.00015 0.00015 0.00014 0.00014 0.00013 0.00013 0.00012 0.00012 0.00011
-3.5 0.00023 0.00022 0.00022 0.00021 0.00020 0.00019 0.00019 0.00018 0.00017 0.00017
-3.4 0.00034 0.00032 0.00031 0.00030 0.00029 0.00028 0.00027 0.00026 0.00025 0.00024
-3.3 0.00048 0.00047 0.00045 0.00043 0.00042 0.00040 0.00039 0.00038 0.00036 0.00035
-3.2 0.00069 0.00066 0.00064 0.00062 0.00060 0.00058 0.00056 0.00054 0.00052 0.00050
-3.1 0.00097 0.00094 0.00090 0.00087 0.00084 0.00082 0.00079 0.00076 0.00074 0.00071
-3.0 0.00135 0.00131 0.00126 0.00122 0.00118 0.00114 0.00111 0.00107 0.00103 0.00100
-2.9 0.00187 0.00181 0.00175 0.00169 0.00164 0.00159 0.00154 0.00149 0.00144 0.00139
-2.8 0.00256 0.00248 0.00240 0.00233 0.00226 0.00219 0.00212 0.00205 0.00199 0.00193
-2.7 0.00347 0.00336 0.00326 0.00317 0.00307 0.00298 0.00289 0.00280 0.00272 0.00264
-2.6 0.00466 0.00453 0.00440 0.00427 0.00415 0.00402 0.00391 0.00379 0.00368 0.00357
-2.5 0.00621 0.00604 0.00587 0.00570 0.00554 0.00539 0.00523 0.00508 0.00494 0.00480
-2.4 0.00820 0.00798 0.00776 0.00755 0.00734 0.00714 0.00695 0.00676 0.00657 0.00639
-2.3 0.01072 0.01044 0.01017 0.00990 0.00964 0.00939 0.00914 0.00889 0.00866 0.00842
-2.2 0.01390 0.01355 0.01321 0.01287 0.01255 0.01222 0.01191 0.01160 0.01130 0.01101
-2.1 0.01786 0.01743 0.01700 0.01659 0.01618 0.01578 0.01539 0.01500 0.01463 0.01426
-2.0 0.02275 0.02222 0.02169 0.02118 0.02067 0.02018 0.01970 0.01923 0.01876 0.01831
-1.9 0.02872 0.02807 0.02743 0.02680 0.02619 0.02559 0.02500 0.02442 0.02385 0.02330
-1.8 0.03593 0.03515 0.03438 0.03362 0.03288 0.03216 0.03144 0.03074 0.03005 0.02938
-1.7 0.04456 0.04363 0.04272 0.04181 0.04093 0.04006 0.03920 0.03836 0.03754 0.03673
-1.6 0.05480 0.05370 0.05262 0.05155 0.05050 0.04947 0.04846 0.04746 0.04648 0.04551
-1.5 0.06681 0.06552 0.06425 0.06301 0.06178 0.06057 0.05938 0.05821 0.05705 0.05592
-1.4 0.08076 0.07927 0.07780 0.07636 0.07493 0.07353 0.07214 0.07078 0.06944 0.06811
-1.3 0.09680 0.09510 0.09342 0.09176 0.09012 0.08851 0.08691 0.08534 0.08379 0.08226
-1.2 0.11507 0.11314 0.11123 0.10935 0.10749 0.10565 0.10383 0.10204 0.10027 0.09852
-1.1 0.13566 0.13350 0.13136 0.12924 0.12714 0.12507 0.12302 0.12100 0.11900 0.11702
-1.0 0.15865 0.15625 0.15386 0.15150 0.14917 0.14686 0.14457 0.14231 0.14007 0.13786
-0.9 0.18406 0.18141 0.17878 0.17618 0.17361 0.17105 0.16853 0.16602 0.16354 0.16109
-0.8 0.21185 0.20897 0.20611 0.20327 0.20045 0.19766 0.19489 0.19215 0.18943 0.18673
-0.7 0.24196 0.23885 0.23576 0.23269 0.22965 0.22663 0.22363 0.22065 0.21769 0.21476
-0.6 0.27425 0.27093 0.26763 0.26434 0.26108 0.25784 0.25462 0.25143 0.24825 0.24509
-0.5 0.30853 0.30502 0.30153 0.29805 0.29460 0.29116 0.28774 0.28434 0.28095 0.27759
-0.4 0.34457 0.34090 0.33724 0.33359 0.32997 0.32635 0.32276 0.31917 0.31561 0.31206
-0.3 0.38209 0.37828 0.37448 0.37070 0.36692 0.36317 0.35942 0.35569 0.35197 0.34826
-0.2 0.42074 0.41683 0.41293 0.40904 0.40516 0.40129 0.39743 0.39358 0.38974 0.38590
-0.1 0.46017 0.45620 0.45224 0.44828 0.44433 0.44038 0.43644 0.43250 0.42857 0.42465
-0.0 0.50000 0.49601 0.49202 0.48803 0.48404 0.48006 0.47607 0.47209 0.46811 0.46414
Calculador de Java de Probabilidades Normales (solamente para navegadores de Microsoft 2.0+/Netscape 2.0+/Java Script)
Para encontrar el área P debajo de la curva de probabilidad normal N(promedio, desviacióon típica) encima de la integral (izquierda, derecha), esciba los cuatros parámetros y presione "Calcule". La curva normal estandar N(0,1) tiene un promedio=0 y d.t.=1. Use -inf y +inf para límites infinitos.
límite izquierdo límite derecho promedio desviacióon típica
CURVAS
(ver también Secciones Cónicas) Punto
x^2 + y^2 = 0 Círculo
x^2 + y^2 = r^2
Elipse
x^2 / a^2 + y^2 / b^2 = 1 Elipse
x^2 / b^2 + y^2 / a^2 = 1 Hipérbola
x^2 / a^2 - y^2 / b^2 = 1
Parábola
4px = y^2 Parábola
4py = x^2 Hipérbola
y^2 / a^2 - x^2 / b^2 = 1
Para mover cada función al centro (j, k) en vez de (0,0), suplante cada término de x con un (x-j) y cada términdo de y con un (y-k) para obtener la ecación deseada.
TEOREMAS NO DEMOSTRADOS
zeta(s) = 1/1s + 1/2s + 1/3s + ... (s = a + it) todos los 0's de zeta(s) en tira 0<=a<=1 yacen en la línea central a=1/2
Números Primos Mellizos ocurren infinitamente
Números Primos Mellizos son primos que están distanciados dos enteros. Ejemplos: 5 & 7, 17 & 19, 101 & 103
El Postulados de Goldbach
Todos los pares >2 pueden ser expresando como la suma de dos primos.
4=2+2, 6=3+3, 8=3+5, 10=5+5, 12=5+7, .. , 100=3+97, ...
El Postulado Paralelo de Euclides
Por un punto, no situado en una línea dada, pasa exactamente una línea paralela a la línea dada. (Pero después vienen esas personas no euclideanas...)
(k=1..) 1/kn = ?
Aunque otros habían descubriendo que está expresión puede con PI2 / 6 cuando n=2, PI4 / 90 cuando n = 4 y soluciones semejantes para todos los valores pares posibles de n, nadie ha descubierto un valor exacto cuando n es un impar (3, 5, 7, ...) (note: cuando n=1, la suma no converge, pero tiene una relación con la constante gamma).
COMPLEJIDAD
Operaciones Básicas
i = (-1)
i^2 = -1
1 / i = -i
i^(4k) = 1; i^(4k+1) = i; i^(4k+2) = -1; i^(4k+3) = -i (k = un entero)
( i ) = (1/2)+ (1/2) i
Definiciones de Funciones y Operaciones Complejas
(a + bi) + (c + di) = (a+c) + (b + d) i
(a + bi) (c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad +bc) i
1/(a + bi) = a/(a^2 + b^2) - b/(a^2 + b^2) i
(a + bi) / (c + di) = (ac + bd)/(c^2 + d^2) + (bc - ad)/(c^2 +d^2) i
a2 + b2 = (a + bi) (a - bi) (la suma de cuadrados)
e^(i ) = cos + i sen
n^(a + bi) = (cos(b ln n) + i sen(b ln n))n^a
si z = r(cos + i sen ) pues z^n = r^n ( cos n+ i sen n )(El Teorema de DeMoivre)
si w = r(cos + i sen ); n=un entero. entonces hay n, nth raices complejas (z) de w para k=0,1,..n-1:
z(k) = r^(1/n) [ cos( (+ 2(PI)k)/n ) + i sen( (+ 2(PI)k)/n ) ]
si z = r (cos + i sen ) pues ln(z) = ln r + i
sen(a + bi) = sen(a)cosh(b) + cos(a)senh(b) i
cos(a + bi) = cos(a)cosh(b) - sen(a)senh(b) i
tan(a + bi) = ( tan(a) + i tanh(b) ) / ( 1 - i tan(a) tanh(b)) = ( sech^2(b)tan(a) + sec^2(a)tanh(b) i ) / (1 + tan^2(a)tanh^2(b))
VECTORES
|
|
k
k
R S= |R| |S| cos ( = el ángulo entre los)
R S= S R
(a R) (bS) = (ab) R S
R (S + T)= R S+ R T
R R = |R| 2
|R x S| = |R| |S| sen ( = el ángulo entre los dos vectores). La dirección de R x S es perpendicular a A & B y según a la ley de mano derecha.
| i j k |
R x S = | r1 r2 r3 | = / |r2 r3| |r3 r1| |r1 r2| \
| s1 s2 s3 | \ |s2 s3| , |s3 s1| , |s1 s2| /
S x R = - R x S
(a R) x S = R x (a S) = a (Rx S)
R x (S + T) = R x S + Rx T
R x R = 0
Si a, b, c = los ángulos entre los vectores de unidad i, j,k y R Pues los cosenos de dirección son definidos por:
cos a = (R i) / |R|; cos b = (R j) / |R|; cos c = (R k) / |R|
|R x S| = El área del paralelográmo con lados R y S.
El componente de R en la dirección de S = |R|cos = (R S) / |S| (resultado escalar)
El proyección de R el la dirección de S = |R|cos = (R S) S/ |S| 2 (resultado vector)
CONSTANTES
EXPANSIONES DE PI
Descubridor: Arquímedes (287-212 BC) averiguó que

PI = 3. 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 ...
La Fórmula de Vieta
2/PI =2/2 *
( 2 +
2 )/2 *
(2 + (
( 2 +
2) ) )/2 * ...c
La Fómula de Leibnitz
PI/4 = 1/1 - 1/3 + 1/5 - 1/7 + ...
El Producto de Wallis
PI/2 = 2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * ...2/PI = (1 - 1/2^2)(1 - 1/4^2)(1 - 1/6^2)...
La Fórmula de Lord Brouncker
4/PI = 1 + 1 ---------------- 2 + 3^2 ------------ 2 + 5^2 --------- 2 + 7^2 ...
(PI^2)/8 = 1/1^2 + 1/3^2 + 1/5^2 + ...
(PI^2)/24 = 1/2^2 + 1/4^2 + 1/6^2 + ...
(PI^2)/6 =(n = 1..
) 1/n^2 = 1/1^2 + 1/2^2 + 1/3^2 + ...
(o mas generalmente...)
(n = 1..
) 1/n^(2k) = (-1)^(k-1) PI^(2k) 2^(2k) B(2k) / ( 2(2k)!)
B(k) = el k th Número Bernoulli. ej. B0=1 B1=-1/2 B2=1/6 B4=-1/30 B6=1/42 B8=-1/30 B10=5/66. Números Bernoulli adicionales se definen como (n 0)B0 + (n 1)B1 + (n 2)B2 + ... + (n (n-1))B(N-1) = 0 presumiendo que todos los Números Impares de Bernoulli >1 son = 0. (n k) = coeficiente de binómico = n!/(k!(n-k)!)
e = 2.7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 ...
e = lim (n -> 0) (1 + n)(1/n) ó e = lim (n ->
) (1 + 1/n)n
e =
(k=0..
) 1 / k!
gamma =
= 0.5772156649 0153286061 ...
= lim (n->
) ( 1 + 1/2 + 1/3 + 1/4 + ... + 1/n - ln(n) ) = 0.5772156649...
= -
e^-x ln x dx
i =
(-1)
i^2 = -1
1 / i = -i
i^(4k) = 1; i^(4k+1) = i; i^(4k+2) = -1; i^(4k+3) = -i (k = un entero)
( i ) =
(1/2)+
(1/2) i
HIPERBÓLICAS
Definiciones de Funciones Hiperbólicas
senh(x) = ( e x - e -x )/2csch(x) = 1/senh(x) = 2/( e x - e -x )
cosh(x) = ( e x + e -x )/2
sech(x) = 1/cosh(x) = 2/( e x + e -x )
tanh(x) = senh(x)/cosh(x) = ( e x - e -x )/( e x + e -x )
coth(x) = 1/tanh(x) = ( e x + e -x)/( e x - e -x )

cosh 2(x) - senh 2(x) = 1
tanh 2(x) + sech 2(x) = 1
coth 2(x) - csch 2(x) = 1

Definiciones de Funciones Hiperbólicas Inversas
arcsenh(z) = ln( z + (z 2 + 1) )
(z 2 + 1) )arccosh(z) = ln( z 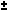
 (z 2 - 1) )
(z 2 - 1) )
arctanh(z) = 1/2 ln( (1+z)/(1-z) )
arccsch(z) = ln( (1+ (1+z 2) )/z )
(1+z 2) )/z )
arcsech(z) = ln( (1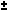
 (1-z 2) )/z )
(1-z 2) )/z )
arccoth(z) = 1/2 ln( (z+1)/(z-1) )

Relaciones con las Funciones Trigonometricas
senh(z) = -i sen(iz)csch(z) = i csc(iz)
cosh(z) = cos(iz)
sech(z) = sec(iz)
tanh(z) = -i tan(iz)
coth(z) = i cot(iz)
TABLAS
I = 3.141592... (aproximadamente a 22/7 = 3.1428)
radianes = grados x PI / 180 (conversión desde grados a radianes)
grados = radianes x 180 / PI (conversión desde radianes a grados)
| Rad | Deg | Sen | Cos | Tan | Csc | Sec | Cot | ||
|---|---|---|---|---|---|---|---|---|---|
| .0000 | 00 | .0000 | 1.0000 | .0000 | ----- | 1.0000 | ----- | 90 | 1.5707 |
| .0175 | 01 | .0175 | .9998 | .0175 | 57.2987 | 1.0002 | 57.2900 | 89 | 1.5533 |
| .0349 | 02 | .0349 | .9994 | .0349 | 28.6537 | 1.0006 | 28.6363 | 88 | 1.5359 |
| .0524 | 03 | .0523 | .9986 | .0524 | 19.1073 | 1.0014 | 19.0811 | 87 | 1.5184 |
| .0698 | 04 | .0698 | .9976 | .0699 | 14.3356 | 1.0024 | 14.3007 | 86 | 1.5010 |
| .0873 | 05 | .0872 | .9962 | .0875 | 11.4737 | 1.0038 | 11.4301 | 85 | 1.4835 |
| .1047 | 06 | .1045 | .9945 | .1051 | 9.5668 | 1.0055 | 9.5144 | 84 | 1.4661 |
| .1222 | 07 | .1219 | .9925 | .1228 | 8.2055 | 1.0075 | 8.1443 | 83 | 1.4486 |
| .1396 | 08 | .1392 | .9903 | .1405 | 7.1853 | 1.0098 | 7.1154 | 82 | 1.4312 |
| .1571 | 09 | .1564 | .9877 | .1584 | 6.3925 | 1.0125 | 6.3138 | 81 | 1.4137 |
| .1745 | 10 | .1736 | .9848 | .1763 | 5.7588 | 1.0154 | 5.6713 | 80 | 1.3953 |
| .1920 | 11 | .1908 | .9816 | .1944 | 5.2408 | 1.0187 | 5.1446 | 79 | 1.3788 |
| .2094 | 12 | .2079 | .9781 | .2126 | 4.8097 | 1.0223 | 4.7046 | 78 | 1.3614 |
| .2269 | 13 | .2250 | .9744 | .2309 | 4.4454 | 1.0263 | 4.3315 | 77 | 1.3439 |
| .2443 | 14 | .2419 | .9703 | .2493 | 4.1336 | 1.0306 | 4.0108 | 76 | 1.3265 |
| .2618 | 15 | .2588 | .9659 | .2679 | 3.8637 | 1.0353 | 3.7321 | 75 | 1.3090 |
| .2793 | 16 | .2756 | .9613 | .2867 | 3.6280 | 1.0403 | 3.4874 | 74 | 1.2915 |
| .2967 | 17 | .2924 | .9563 | .3057 | 3.4203 | 1.0457 | 3.2709 | 73 | 1.2741 |
| .3142 | 18 | .3090 | .9511 | .3249 | 3.2361 | 1.0515 | 3.0777 | 72 | 1.2566 |
| .3316 | 19 | .3256 | .9455 | .3443 | 3.0716 | 1.0576 | 2.9042 | 71 | 1.2392 |
| .3491 | 20 | .3420 | .9397 | .3640 | 2.9238 | 1.0642 | 2.7475 | 70 | 1.2217 |
| .3665 | 21 | .3584 | .9336 | .3839 | 2.7904 | 1.0711 | 2.6051 | 69 | 1.2043 |
| .3840 | 22 | .3746 | .9272 | .4040 | 2.6695 | 1.0785 | 2.4751 | 68 | 1.1868 |
| .4014 | 23 | .3907 | .9205 | .4245 | 2.5593 | 1.0864 | 2.3559 | 67 | 1.1694 |
| .4189 | 24 | .4067 | .9135 | .4452 | 2.4586 | 1.0946 | 2.2460 | 66 | 1.1519 |
| .4363 | 25 | .4226 | .9063 | .4663 | 2.3662 | 1.1034 | 2.1445 | 65 | 1.1345 |
| .4538 | 26 | .4384 | .8988 | .4877 | 2.2812 | 1.1126 | 2.0503 | 64 | 1.1170 |
| .4712 | 27 | .4540 | .8910 | .5095 | 2.2027 | 1.1223 | 1.9626 | 63 | 1.0996 |
| .4887 | 28 | .4695 | .8829 | .5317 | 2.1301 | 1.1326 | 1.8807 | 62 | 1.0821 |
| .5061 | 29 | .4848 | .8746 | .5543 | 2.0627 | 1.1434 | 1.8040 | 61 | 1.0647 |
| .5236 | 30 | .5000 | .8660 | .5774 | 2.0000 | 1.1547 | 1.7321 | 60 | 1.0472 |
| .5411 | 31 | .5150 | .8572 | .6009 | 1.9416 | 1.1666 | 1.6643 | 59 | 1.0297 |
| .5585 | 32 | .5299 | .8480 | .6249 | 1.8871 | 1.1792 | 1.6003 | 58 | 1.0123 |
| .5760 | 33 | .5446 | .8387 | .6494 | 1.8361 | 1.1924 | 1.5399 | 57 | .9948 |
| .5934 | 34 | .5592 | .8290 | .6745 | 1.7883 | 1.2062 | 1.4826 | 56 | .9774 |
| .6109 | 35 | .5736 | .8192 | .7002 | 1.7434 | 1.2208 | 1.4281 | 55 | .9599 |
| .6283 | 36 | .5878 | .8090 | .7265 | 1.7013 | 1.2361 | 1.3764 | 54 | .9425 |
| .6458 | 37 | .6018 | .7986 | .7536 | 1.6616 | 1.2521 | 1.3270 | 53 | .9250 |
| .6632 | 38 | .6157 | .7880 | .7813 | 1.6243 | 1.2690 | 1.2799 | 52 | .9076 |
| .6807 | 39 | .6293 | .7771 | .8098 | 1.5890 | 1.2868 | 1.2349 | 51 | .8901 |
| .6981 | 40 | .6428 | .7660 | .8391 | 1.5557 | 1.3054 | 1.1918 | 50 | .8727 |
| .7156 | 41 | .6561 | .7547 | .8693 | 1.5243 | 1.3250 | 1.1504 | 49 | .8552 |
| .7330 | 42 | .6691 | .7431 | .9004 | 1.4945 | 1.3456 | 1.1106 | 48 | .8378 |
| .7505 | 43 | .6820 | .7314 | .9325 | 1.4663 | 1.3673 | 1.0724 | 47 | .8203 |
| .7679 | 44 | .6947 | .7193 | .9657 | 1.4396 | 1.3902 | 1.0355 | 46 | .8029 |
| .7854 | 45 | .7071 | .7071 | 1.0000 | 1.4142 | 1.4142 | 1.0000 | 45 | .7854 |
| Cos | Sin | Cot | Sec | Csc | Tan | Deg | Rad |
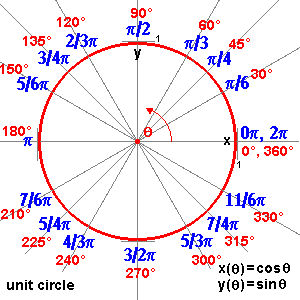
| ángulo (grados) | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 | 360 = 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ángulo (radianes) | 0 | PI/6 | PI/4 | PI/3 | PI/2 | 2/3PI | 3/4PI | 5/6PI | PI | 7/6PI | 5/4PI | 4/3PI | 3/2PI | 5/3PI | 7/4PI | 11/6PI | 2PI = 0 |
| sen(a) |  (0/4) (0/4) |  (1/4) (1/4) |  (2/4) (2/4) |  (3/4) (3/4) |  (4/4) (4/4) |  (3/4) (3/4) |  (2/4) (2/4) |  (1/4) (1/4) |  (0/4) (0/4) | - (1/4) (1/4) | - (2/4) (2/4) | - (3/4) (3/4) | - (4/4) (4/4) | - (3/4) (3/4) | - (2/4) (2/4) | - (1/4) (1/4) |  (0/4) (0/4) |
| cos(a) |  (4/4) (4/4) |  (3/4) (3/4) |  (2/4) (2/4) |  (1/4) (1/4) |  (0/4) (0/4) | - (1/4) (1/4) | - (2/4) (2/4) | - (3/4) (3/4) | - (4/4) (4/4) | - (3/4) (3/4) | - (2/4) (2/4) | - (1/4) (1/4) |  (0/4) (0/4) |  (1/4) (1/4) |  (2/4) (2/4) |  (3/4) (3/4) |  (4/4) (4/4) |
| tan(a) |  (0/4) (0/4) |  (1/3) (1/3) |  (2/2) (2/2) |  (3/1) (3/1) |  (4/0) (4/0) | - (3/1) (3/1) | - (2/2) (2/2) | - (1/3) (1/3) | - (0/4) (0/4) |  (1/3) (1/3) |  (2/2) (2/2) |  (3/1) (3/1) |  (4/0) (4/0) | - (3/1) (3/1) | - (2/2) (2/2) | - (1/3) (1/3) |  (0/4) (0/4) |